보외법 = 외삽법 = 지금까지 경향을 보고 밖(미래/과거)의 값을 추정한다는 말.
고등학교 말년에서 대학교 신입까지 수준으로 설명하면 이렇다.
수학은 원래 실용적이고 구체적인 문제를 풀다가 발달한 것인데,
사회 나오면 쓸 일 없는 근의 공식을 외우고 있으니... (인터넷 검색하면 다 나오잖아)
정말 수학을 재미 없게 가르치고 있다.
점이 2개 있으면 1차 다항식, 3개 있으면 2차 다항식, 4개 있으면 3차 다항식으로 사이 값을 추정할 수 있다. 그럼 N+1개 점의 데이터가 있다고 하면 다음과 같은 다항식을 구할 수 있을 것이다. 계수를 구하는 방법은 가우스 소거법이다. 기타 라그랑주 다항식을 구하는 아주 복잡한 계산의 보간법도 있다. 어차피 보간법이란 것이 대충 추측해서 넣는 것이라 최적의 보간법이란 것이 없다. 그런데 대학 수학에선 신기하게도 다항식으로 어떤 함수의 근사치를 구하는 방법이 있다. 테일러 급수라는 방법으로 컴퓨터에선 삼각 함수, 지수 함수, 로그 함수 등의 값을 계산한다. 다항식 만세!
정말 수학을 재미 없게 가르치고 있다.
1. N차 다항식 보간법
점이 2개 있으면 1차 다항식, 3개 있으면 2차 다항식, 4개 있으면 3차 다항식으로 사이 값을 추정할 수 있다. 그럼 N+1개 점의 데이터가 있다고 하면 다음과 같은 다항식을 구할 수 있을 것이다. 계수를 구하는 방법은 가우스 소거법이다. 기타 라그랑주 다항식을 구하는 아주 복잡한 계산의 보간법도 있다. 어차피 보간법이란 것이 대충 추측해서 넣는 것이라 최적의 보간법이란 것이 없다. 그런데 대학 수학에선 신기하게도 다항식으로 어떤 함수의 근사치를 구하는 방법이 있다. 테일러 급수라는 방법으로 컴퓨터에선 삼각 함수, 지수 함수, 로그 함수 등의 값을 계산한다. 다항식 만세!
y = a + bx¹ + cx² + dx³ + ex⁴+ ... + mxⁿ
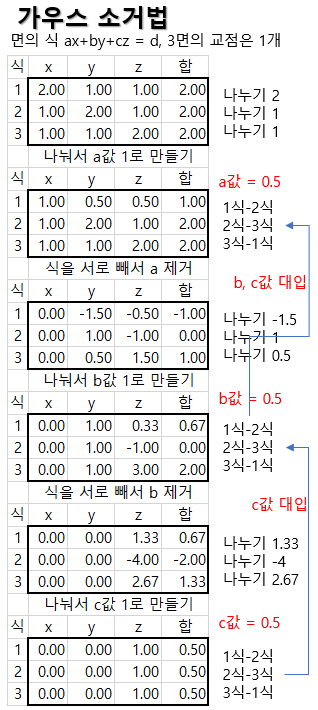
가우스 소거법이란?
위의 수식에서 a, b, c, d, e 등의 계수를 구해야 한다. 방법은 모든 x, y에 대해 값을 대입해서 수식 N+1개를 만든 후에, 각 수식에 특정 값을 곱하거나 나누어 특정 계수만 남긴다. 예를 들어 3a + 2b + 4c = 5 라고 하면 3을 나누면 a + 2/3b + 4/3c = 5/3이 되는 식이다. a만 대머리가 된다. 그리고 수식들을 서로 빼면 특정 계수 a가 사라진다. 이렇게 계수를 줄이다 보면 어떤 계수의 값이 정해진다. 그 값을 이용해서 나머지 계수도 차례차례 구하는 방식이다.
어떤 임의의 함수가 있을 때 이것을 무한 주파수 + 무한 진폭의 Sin, Cos의 합으로 표현한다는 개념이 푸리에 변환이고, 무한 차수 + 무한 계수의 다항식의 합으로 표현한다는 개념이 테일러급수이다. 위키 백과(이공계 쪽 내용은 믿을만함)에서 검색해 보라.
Excel에서 Cos함수를 6차 다항식으로 근사시켜 보았다. Cos과 Sin은 반복되는 값이고 서로 각도만 다르고 0~45도까지 값만 구하면 부호만 다르기 때문에 결국 다항식으로 Cos/Sin 함수를 계산할 수 있다. 그뿐만 아니라 원주율도 다항식으로 계산할 수 있다. 매우 놀랍다. 결국 4칙 연산만 알면 모든 것을 구한다.
지수와 로그 함수는 서로 엮여 있다. 지수 함수를 계산할 때는 e값을 기준으로 바꾸어 계산해야 하는데 그렇게 하려면 어쩔 수 없이 로그 값을 먼저 계산해야 한다. (여기 공식으로 보면 그렇다.) 다행히 컴퓨터에선 모든 수를 2의 배수로 표현하기 때문에 ln2만 알고 있으면 나머지도 계산 된다. 결국 지수와 로그 함수는 ln2의 배수로 계산 된다. 다항식 만세!
Excel에서 Cos함수를 6차 다항식으로 근사시켜 보았다. Cos과 Sin은 반복되는 값이고 서로 각도만 다르고 0~45도까지 값만 구하면 부호만 다르기 때문에 결국 다항식으로 Cos/Sin 함수를 계산할 수 있다. 그뿐만 아니라 원주율도 다항식으로 계산할 수 있다. 매우 놀랍다. 결국 4칙 연산만 알면 모든 것을 구한다.
지수와 로그 함수는 서로 엮여 있다. 지수 함수를 계산할 때는 e값을 기준으로 바꾸어 계산해야 하는데 그렇게 하려면 어쩔 수 없이 로그 값을 먼저 계산해야 한다. (여기 공식으로 보면 그렇다.) 다행히 컴퓨터에선 모든 수를 2의 배수로 표현하기 때문에 ln2만 알고 있으면 나머지도 계산 된다. 결국 지수와 로그 함수는 ln2의 배수로 계산 된다. 다항식 만세!
2. 1차 다항식 보간법 = 선형 보간법
점이 2개 있을 때 그 사이를 직선으로 보고 중간 값을 구한다. 그러니까 각 구간을 1차 다항식으로 근시사키는 것이다. 점이 2개 있으면 1차 다항식의 기울기와 절편을 구할 수 있다. 이런 것을 보간법이라고 하지는 않겠지? 직선이라고 해서 영어에선 linear/리니어라고 부른다. 이건 거의 밋밋한 곡선에 대해 적용한다.
y = a + bx
점 A와 B 2개의 점이 있을 때 A를 0점으로 놓고 상대적인 값을 구한 후에 나중에 절대적인 값으로 바꾸면 계산이 쉽다. 그래서 A(0,0)으로 놓고 B(Δx, Δy)로 놓고 계산한다. 그러면 다음과 같이 간단하게 바뀐다.
a = 0여기서 구한 계수를 이용해서 상대 값에서 보간 공식을 구하면 아래와 같다.
b = Δy/Δx
(y – y₁) = b(x – x₁)
y = bx + (y₁ - bx₁)
절대 값으로 결과는 (x + x₁, y + y₁)이다.
3. 2차 다항식 보간법
점이 3개 있을 때는 2차 다항식을 구하면 되는데 n개의 점이 있을 때 각 구간을 2차 다항식으로 근사시켜 중간 값을 구할 수 있다. 이 경우는 2개의 점과 2개 지점의 기울기를 일치시켜야 부드러운 곡선이 얻어진다. 2개의 점과 1개의 기울기만 있어도 2차 다항식을 구할 수 있기 때문에 기울기는 어느 한 지점을 기준으로 다른 지점으로 전파된다. 제곱은 정사각형과 관계있기 때문에 영어에선 square/스퀘어라고 부른다. 최초 지점의 기울기는 적당하게 알아서 지정한다. 아래 수식에서 a, b, c만 구하면 된다. 2차 다항식 보간법의 문제는 어떤 곡선에선 부드럽게 연결되지 않고 갑자기 꺾일 수도 있다는 것이다. 이것도 거의 밋밋한 곡선에 대해 적용한다. 그냥 선형보간에 비해 오차가 적도록 적용하는 것이다.
y₁= a + bx₁+ cx²₁
y₂= a + bx₂+ cx²₂
s₁= b + 2cx₁(1차 미분 = 기울기 지정)
s₂= b + 2cx₂(1차 미분 = 기울기 파생)
역시 점 A와 B에서 점 A를 0점으로 놓고 상대적 값으로 계산하면 아래와 간단하게 정리 된다. A(0,0), B(Δx, Δy)이고 기울기만 그대로 유지한다.
a = 0역시 이렇게 구한 계수를 대입해서 상대 값에서 보간 공식을 구하면 아래와 같다.
b = s₁ = 지정값
c = (Δy - Δx*s₁)/Δx²
s₂= s₁+ 2c*Δx = 파생값 → 다음 지점의 기울기로 전파
(y - y₁) = b*(x - x₁) + c*(x - x₁)²
y = cx² + (b – 2cx₁)x + (y₁+ cx²₁– bx₁)
절대 값으로 결과는 (x + x₁, y + y₁)이다.
4. 3차 다항식 보간법 = 큐빅 스플라인 보간법
점이 4개 있으면 3차 다항식을 구하면 되는데 역시 n개의 점이 있다고 했을 때 2개 점 사이를 3차 다항식으로 근사시키는 방법이 있다. 부드럽게 연결되려면 양쪽 지점의 기울기도 일치시켜야 한다. 2개 지점을 알기 때문에 양쪽의 기울기만 지정하면 된다. 3차는 입방체를 의미하기 때문에 영어에선 cubic/큐빅이라고 부른다. 입방체는 정6면체를 말한다. spline/스플라인은 운형(雲形)자를 뜻하는데 구름 모양으로 말리는 형상을 말한다. 아마도 곡선을 이어 붙이는데서 나온 이름이 아닐까? 아래 수식에서 a, b, c, d를 구하면 된다. 좀 더 자연스럽게 연결시키려면 양쪽의 2차 미분 값도 일치시키면 될 것 같은데 그렇게 안 된다. 2차 미분의 경우 자동으로 파생되어 결정된다. 이것도 역시 거의 밋밋한 곡선에 대해 적용해야 오차가 적다. 비교적 급하게 변하는 곡선에 적용해도 되지만 오차가 커질 것이다.
y₁= a + bx¹₁+ cx²₁+ dx³₁
y₂= a + bx¹₂+ cx²₂+ dx³₂
s₁= b + 2cx¹₁+ 3dx²₁(1차 미분 = 기울기 지정)
s₂= b + 2cx¹₂+ 3dx²₂(1차 미분 = 기울기 지정)
m₁= 2c + 6dx₁(2차 미분 파생)
m₂= 2c + 6dx₂(2차 미분 파생)
앞에서와 같은 방법으로 상대적 차이로 계산을 하면 아래와 같이 간단하게 정리 된다. 적용할 때는 다시 절대적 값으로 바꾼다. (아 씨발 미분 공식도 까먹었다. 늙으면 죽어야 돼!)
보통 직선에 가까운 밋밋한 곡선을 이루는 것은 3차 다항식 보간까지 구하면 된다. 앞의 1차, 2차 보간법 같은 것은 잊어라.
a = 0
b = s₁ = 지정값
(Δy - b*Δx) = c*Δx² + d*Δx³
(s₂- s₁) = 2c*Δx + 3d*Δx²
c = {3(Δy - b*Δx) - (s₂- s₁)Δx}/Δx²
d = {(s₂- s₁)Δx - 2(Δy - b*Δx)}/Δx³
m₁= 2c = 파생값
m₂= m₁+ 6d*Δx = 파생값
이렇게 구한 계수를 대입해서 절대 값에서 보간 공식을 구하면 너무 복잡하니까 상대적인 값으로 계산을 한 후에 기준 좌표의 값을 더해주는 방식을 사용한다. 상대 좌표(지역 좌표)로 계산한 후에 절대 좌표(세계 좌표)로 바꾸는 것은 3D 그래픽에서도 이용하는 방법이다. 한 번에 계산하려고 하면 너무 복잡하다.
(y - y₁) = b*(x - x₁) + c*(x - x₁)² + d*(x - x₁)³
y = y₁ + .... (x의 계수 형태로 풀면 복잡)
보통 직선에 가까운 밋밋한 곡선을 이루는 것은 3차 다항식 보간까지 구하면 된다. 앞의 1차, 2차 보간법 같은 것은 잊어라.
5. 기울기 지정
a-b-c 3개의 점이 있다고 할 경우 b의 기울기는 다음과 같이 그냥 정한다.
{(a-b)/Δx + (b-c)/Δx}/2 = (a-c)/2Δx = 양쪽 기울기 평균
6. 보외법
이건 어떤 경향성이 있는 경우 통한다. 예를 들어 sin/cos처럼 진동하거나 지수 함수처럼 일정 비율로 증감하는 경우에 예측하기 좋다. 예측이 불가능한 것은 말 그대로 예측이 안 되니까 마음대로 해라. Excel을 이용하면 다항식, 지수함수, 로그함수 등을 자동으로 근사시켜 찾아주기 때문에 보간법(내삽법), 보외법(외삽법) 적용하기 쉬울 것이다.
내가 대학 수학을 엉터리로 공부해서 대학 수학 수준으로 설명하지는 못 하겠다. 대학 수학이 그렇게 어려운 것이 아니다. (내 동생은 고등학교 때 대학 수학 공부해서 문제를 아주 쉽게 풀었다. 내가 생각보다 쉬우니 공부해 보라고 했지.) 고등학교 선생들처럼 가르치면 대학 수학도 아주 쉽게 배울 수 있다. 그런데 우리 거만한 교수님들께서 (아니면 부잣집 자식이라서 쉽게 외국 대학을 나왔는지) 그렇게 쉽게 가르쳐 주지 않으니 어려울 수밖에 없다. 알면 아무것도 아닌데 모르니 어렵게 보일 뿐이다.
달리기가 느려도 결국 도착지점에 도달하듯이 머리가 나빠도 결국 이해는 한다. 우린 다리가 짧아서 느린 것뿐이다. 토끼가 1등을 하고 거북이가 꼴찌를 하겠지만 결국 같은 경지에 도달한다. 그러니까 너무 SKY에 겁먹지 마라. 이명박처럼 2류 대학 나오나 박근혜처럼 3류 대학 나오나 무능하고 부도덕하기는 별 차이도 없고, 김영삼처럼 부잣집 자식이라서 공부 하나도 안 하고 대통령까지 하는 것도 가능하며, 비록 고졸이지만 김대중, 노무현처럼 지적인 대통령도 배출하는 참으로 기회가 많은 나라다. 서울대 검찰 출신 꼴통도 있던데...
달리기가 느려도 결국 도착지점에 도달하듯이 머리가 나빠도 결국 이해는 한다. 우린 다리가 짧아서 느린 것뿐이다. 토끼가 1등을 하고 거북이가 꼴찌를 하겠지만 결국 같은 경지에 도달한다. 그러니까 너무 SKY에 겁먹지 마라. 이명박처럼 2류 대학 나오나 박근혜처럼 3류 대학 나오나 무능하고 부도덕하기는 별 차이도 없고, 김영삼처럼 부잣집 자식이라서 공부 하나도 안 하고 대통령까지 하는 것도 가능하며, 비록 고졸이지만 김대중, 노무현처럼 지적인 대통령도 배출하는 참으로 기회가 많은 나라다. 서울대 검찰 출신 꼴통도 있던데...
친일선동언론에서 다음과 같은 얘기가 나오면 그냥 무시해라. 우리 관심을 다른 곳에 돌리기 위한 작전이다. 왜냐하면 이런 내용은 하나 마나 별로 피부에 와 닿는 차이가 없다. 또는 우리가 절대 어떻게 할 수가 없는 일을 거론하는 것이다.
- 동북공정 = 한중일 모두 역사 왜곡하고 있다. 우리도 우리 근현대 역사 왜곡한다.
- 독도망언 = 말로만 떠들지 달라질 내용이 없다. 무인도는 영토로 인정 못 받는다.
- 미군철수 = 전쟁 하지 않을 거면 그게 그거. 80년대말에 좌우대립은 끝났다.
- 전시작전권 = 전쟁 하지 않을 거면 차이 없다. 어차피 전쟁하면 미군이 지휘한다.
- 북핵 = 이건 미국 문제고 우리 문제 아니다. 결자해지 미국이 해결해야 한다.
- 북한인권 = 남한 인권이나 먼저 좀 돌보지 그래? 뭐라 하면 북한이 우리 말 듣냐?
- 남북통일 = 북한의 김씨세습독재와 남한의 친일독재잔당이 망하면 될까? 잊어라.
- 군가산점 = 대부분의 남자들은 어차피 이 혜택을 못 본다. 왜 여기에 목을 매니?
아래 일이 우리에겐 더 중요하다. 우리 삶과 직접적으로 관계있고, 우리가 해결할 수 있는 문제다. 아래 일이 우리가 진짜 관심 가져야 하는 일이다. 북한 안드로메다의 판타지는 필요 없단 말이지. 북한 똥은 나중에 치우고 우리 똥이나 먼저 치우자.
- 민주 = 우리 자유가 걸린 일이다. 깡패 친일독재잔당에 계속 굴복하고 싶니?
- 복지 = 사회보험, 기회균등, 공정경쟁, 공정거래, 공평함, 이런 거 싫어?
- 평화 = 우리 목숨이 걸린 일이다. 가만히 있어도 늙어 죽는데 뭐하러?
- 법치 = 깡패 친일독재잔당은 범법 집단이다. 얘들이 제정신인지 모르겠다.
- 남녀평등 = 여자들 일생이 걸린 일이다. 한 번 사는 인생인데 행복해야지?
- 빈부격차 = 우리 경제 불황 문제다. 이건 공식이다. 빈부격차 = 경제불황
- 고용안정 = 우리 밥줄이 걸린 일이다. 납치/고문/암살 → 모함/벌금 → 밥줄끊기
- 물가안정 = 우리 경제 불황 문제다. 물가상승 = 통화량증가 = 빚(대출)증가
친일독재잔당의 국민 지배 전술은 적반하장 전술과 분열전술이다. 지들이 한 짓을 북한이나 야권에서 했다고 덮어씌우는 것이 적반하장 전술이다. 분열전술은 국민을 분열시켜 서로 싸우게 하는 전술이다. 자신들을 보수우익이라고 하지만 외국인이 보면 비웃는다. 친일파는 매국노이고 독재잔당은 반민주세력, 간신배, 모리배다.
- 야권분열 : 엉뚱한 3등을 띄워서 2등 표를 갉아 먹는다.
- 지역차별 : 호남 vs 영남, 탈북자 vs 남한인 vs 재일교포 vs 조선족
- 사상차별 : 좌파(거지/흥부/서민) vs 우파(부자/놀부/귀족)
- 종교차별 : 천주교(1/8) vs 개독교(1/8) vs 불교(1/4) vs 무종교 vs 좌파
- 신분차별 : 전문직(중인) vs 월급쟁이(평민) vs 노동자(천민)
- 남녀차별 : 공무원이 아니면 써먹지도 못 하는 군가산점으로 싸움을 붙인다.
- 세대차별 : 젊은이(진보) vs 낡은이(꼴보)
정치, 경제, 종교(사상/이념/철학)에서도 수학처럼 정답은 있다. 인문학 계통이 정답이 명쾌하게 나오지 않는 말장난처럼 보여서 정답이 없는 선택 문제라고 오해하는데 분명 정답은 있다. 당신이 좋아하는 여자 스타일, 좋아하는 색상 같은 것이나 정답이 없다. 정치, 경제, 종교는 여러 사람의 삶에 공통적, 객관적 영향을 주기 때문에 정답이 있다. 이 문제는 법에 정답이 있냐는 것과 비슷한 것이다.
정치 얘기는 나중에 보면 유치할 수밖에 없다. 왜냐하면 모든 나라의 정치가 (학문, 예술 등과 비교해서) 가장 뒤떨어진 분야라서 그걸 언급하면 저절로 유치해진다. 그런데 이 유치한 얘기를 안 할 수도 없다. 울며 겨자 먹기로 너무나도 당연한 얘기를 반복해야 한다. 최고로 재미 있는 코미디는 정치/종교이다.
정치 얘기는 나중에 보면 유치할 수밖에 없다. 왜냐하면 모든 나라의 정치가 (학문, 예술 등과 비교해서) 가장 뒤떨어진 분야라서 그걸 언급하면 저절로 유치해진다. 그런데 이 유치한 얘기를 안 할 수도 없다. 울며 겨자 먹기로 너무나도 당연한 얘기를 반복해야 한다. 최고로 재미 있는 코미디는 정치/종교이다.
댓글 없음:
댓글 쓰기