암산은 계산기가 없었던 때에 계산을 빠르고 정확하게 하려고 개발된 요령이다. 암산 요령은 주로 기억력을 활용하는 경우가 많다. 계산뿐만 아니라 인간 두뇌 활동의 기본은 기억이 바탕이 된다. 암산의 가장 첫 단계가 바로 99단 암기다. 여기서 암산은 주로 정수 사칙연산이다.
결론을 말하자면 복잡한 계산은 Excel을 사용하고 간단한 4칙연산은 주산 암산이 최고다. 암산하면 잘 틀린다. 그냥 계산기 써라. 인도 수학이란 것도 주산과 비슷한 원리고 둘을 합하면 계산기 없을 때 천하무적이다. 그러나 중요한 계산은 계산기를 써라.
결론을 말하자면 복잡한 계산은 Excel을 사용하고 간단한 4칙연산은 주산 암산이 최고다. 암산하면 잘 틀린다. 그냥 계산기 써라. 인도 수학이란 것도 주산과 비슷한 원리고 둘을 합하면 계산기 없을 때 천하무적이다. 그러나 중요한 계산은 계산기를 써라.
0. 99단 암기
곱하기, 나누기를 하려면 99단 암기를 해야 한다. 계산을 더 빠르게 한다는 취지에서 10자리까지 포함된 19x19단을 암기한다고 하는데 쓸 데 없는 짓이다. (10+9)*(10+9)로 분해하면 100+90+90+81로 쉽게 계산이 된다. 99단까지 암기하고 주산을 배우는 것이 더 효율적이다. 99단도 거의 1/2만 암기하면 된다. 8x9=9x8=72 같기 때문이다.
0-1. 19단이란?
(10 + a)(10 + b) = 100 + 10(a + b) + ab = 10(10 + a + b) + ab
15*17 = 100 + 10(5+7) + 5*7 = 10(10+5+7) + 35 = = 220 + 35 = 255
10자리가 항상 1이란 특수한 경우에선 수식이 단순해져서 곱하기는 1의 자리 숫자 1회만 하면 되고 나머진 더하기로 바뀐다. 이걸 외울 필요가 있나?
0-2. 보수 이용
곱하기가 물리적으로 가지는 의미를 알면 더 쉽다. 곱하기는 면적을 의미한다. 정사각형 가지고 배치하는 상상을 하면서 면적 계산을 하면 답이 바로 나온다. 어떤 수 A에 5보다 큰 수 B를 곱한다고 하자.
B = 10 - C, C는 B에 대한 10의 보수라고 한다. B가 클 때 작은 C를 사용한다.
A*B = A*(10 – C) = A*10 - AC → 10의 보수를 이용한 방법이다.
3*98 = 3*(100-2) = 300-6 = 294 → 100의 보수를 이용.
B = 10/C, 여기서 C도 B에 대한 보수와 비슷하게 곱하기에서 짝이 된다.
5 = 10/2, 비슷한 개념으로 5와 2는 짝, 5대신 2를 사용한다.
25 = 100/4, 비슷한 개념으로 25대신 4를 쓸 수 있다는 것.
95/5 = 95/10/2 = 95*2/10 = 19
큰 수는 10, 100, 1000, 10000 등의 보수로 바꾸면 계산이 쉬워진다. 이런 식으로 계산할 경우 5미만의 곱셈만 암기하면 된다. 즉 99단 81개를 암기하는 게 아니라 55단 중에 1단 5개를 뺀 20개 중에서 반인 10개만 암기하면 된다는 것.
1. 주산 암산
간단한 사칙연산은 주산을 기계적으로 훈련해서 해결할 수 있다. 이는 손가락 운동 신경에 계산법을 기억시킨 것과 같다. 주산과 99단이 결합하면 큰 수의 사칙연산도 쉽게 된다. 주판은 컴퓨터가 없었을 때 90년대까지 은행에서도 사용하던 수동 계산기였고 아주 오래되고 증명된 방법이다. (컴퓨터는 그 이전에 썼는데 아직 컴퓨터를 믿지 못 하던 시절이라...) 주판을 상상하고 손가락으로 계산을 하는 방식이다. 훈련하면 상당히 큰 수도 명확하게 기억할 수 있다. 그림은 숫자보다 더 잘 기억되기 때문이다. (사진기도 아닌데 어떻게?) 주판에선 5점 돌과 1점 돌 4개로 수를 표현한다.
1-1. 수의 표현
- 0
- 1
- 2
- 3
- 4
- 5 → 5+0
- 6 → 5+1
- 7 → 5+2
- 8 → 5+3
- 9 → 5+4
7+8을 계산할 때는 순간적으로 (5+2)+(5+3)=10+5으로 분해되어 계산된다. 또한 10의 보수라는 것을 이용해서 덧셈과 뺄셈을 한다. 잘 보면 5의 보수도 이용한다. 1점 돌이 더해져 5를 넘기면 처리해야 하기 때문이다. 이걸 머리로 하는 게 아니라 손가락 기억으로 한다. 그래서 무의식 중에 계산이 된다.
A + B = 9, A + B = 10, A + B = 5의 경우 B는 A에 대해서 9, 10, 5의 보수라고 한다. 보수를 합하면 완전해지기 때문에 보수라고 하는 것이다. 즉 완전해지면 한 단계 승진한다. Level-Up하는 것이다. 주판에선 덧셈 결과 5를 넘어가면 5점짜리 하나를 움직여야 한다. 고로 5의 보수를 사용한다. 또한 10을 넘어가면 앞자리에 올림을 해야 하니 10의 보수도 사용한다.
1-2. 보수 이용
A + B = 9, A + B = 10, A + B = 5의 경우 B는 A에 대해서 9, 10, 5의 보수라고 한다. 보수를 합하면 완전해지기 때문에 보수라고 하는 것이다. 즉 완전해지면 한 단계 승진한다. Level-Up하는 것이다. 주판에선 덧셈 결과 5를 넘어가면 5점짜리 하나를 움직여야 한다. 고로 5의 보수를 사용한다. 또한 10을 넘어가면 앞자리에 올림을 해야 하니 10의 보수도 사용한다.
- 10 = 1+9 = 1+(5+4)
- 10 = 2+8 = 2+(5+3)
- 10 = 3+7 = 3+(5+2)
- 10 = 4+6 = 4+(5+1)
- 10 = 5+5 = 5+(5+0)
- 5 = 0+5
- 5 = 1+4
- 5 = 2+3
어차피 4칙연산은 기억이 바탕이고 머리로 기억하나 몸으로 기억하나 마찬가지다. 수학자나 과학자도 배우면 좋다. 수에 대한 감각이 생긴다. 수에 대한 감각이란 하나의 수를 덧셈, 곱셈 성분으로 분해하여 보는 훈련이다. 숫자를 보면 분해하고 싶어지는 이상한 놈들이지?
1-3. 덧셈 뺄셈
인도 수학과 비슷하게 앞자리부터 계산한다는 점이 학교에서 배운 것과 다르다. 뺄셈도 덧셈처럼 앞에서부터 계산을 한다. 거꾸로 계산하느라 틀릴 가능성이 줄어든다. 덧셈이나 뺄셈이나 보수를 이용하면 편리하다. 뺄셈에서 빼는 수가 더 큰 경우는 9의 보수로 바꾸어 더한 후에 다시 9의 보수로 바꾸면 된다. 주산에선 이 경우 약간 다른 방식으로 10의 보수를 이용하지만 원리는 같다. 뭐의 보수를 취하든 상관없다. 두 수보다 크면 된다. 주산의 경우는 앞에서 가상의 1을 빌린 후에 정상적인 뺄셈을 하고 결과를 10의 보수로 읽는 식이다. 5555의 9999의 보수는 4444이지만 주산에선 10000의 보수를 취하니 4445인 것이다.
2. 수의 분해 = 인수 분해 & 자릿수 분해 = 대수학 공식 암기
수를 분해해서 계산하는 방법이 있다. 이건 곱셈과 덧셈으로 분해 가능하다. 곱셈 분해는 소인수 분해라고 한다. 당연히 소수(prime number)들을 많이 암기 하고 있어야 한다. 이런 것을 수학적 감각이라고 한다. 덧셈 분해는 자리수 분해이다. 주로 큰 수의 곱셈에 이용할 수 있다. 예를 들어 56의 제곱을 계산할 때 (50 + 6)² = 100*5² + 10*(2*5*6) + 6² 형태로 덧셈 분해를 하는 경우와 (7*8)² = 7²8² 형태로 소인수 분해 하는 경우가 있을 것이다.
위와 같은 곱셈 공식들을 이용해서 큰 수의 곱셈을 작은 수의 곱셈과 덧셈으로 바꾸는 방법을 인도 수학에서 교묘하게 이용한다. 수학의 힘은 표기법에 있다. 숫자와 수식을 표현하는 방법이 계산과 생각의 효율을 향상시킨 것이다. 즉 수학이란 기호 언어의 힘이다. 무슨 뜻인지 아래를 보면 안다. 왜 표기법/표현법이 중요한지. 위의 곱셈 공식도 세로로 적어 보면 암기 자체가 쉽게 된다. 또한 계산도 쉽다.
2-1. 곱하기 일반
세 자리 수를 곱한다고 하자. 100의 자리 숫자는 X, 10의 자리 숫자는 Y, 1의 자리는 Z일 때
XYZ로 표기하는 방식이다. 곱하기 기호가 생략된 게 아니다. X와 Y를 곱할 때는 X*Y로 명확히 표기한다. 뒤에 붙은 0은 자릿수를 나타낸다. 즉 XYZ = X00+Y0+Z이다.
X, Z가 양수이고 Y가 음수일 경우 X00-Y0+Z = XYZ 형태로 숫자 위나 아래에 바(-)나 점을 찍는다. 이건 10의 보수를 이용한 계산법이다. 일부 숫자가 음수라도 상관 없이 계산할 수 있다. 대수식의 표기를 좀 더 편하게 바꾼 것이다. 즉 학교에서 배운 것을 이 방식으로 풀어 보자.
XY*AB = (X0 + Y)(A0 + B) = (X*A)00 + (X*B + Y*A)0 + YB
84*92 = (8*9)00 + (8*2+4*9)0 + 4*2 = 7200 + 520 + 8 = 7728
84*108 = (8*10)00 + (8*8+4*10)0 + 4*8 = 8000 - 240 - 32 = 7728
96*108 = (9*10)00 + (6*10+9*8)0 + 6*8 = 9000 - 1320 + 48 = 7728
여기서 92 = 100-8 = 108, 84 = 90 - 6 = 96 표기법만 바뀐 위력이다. 수학적으로 깔끔하게 증명되는 보수로 계산하는 방식이다. 아라비아 숫자가 원래 인도 것이다. 자릿수 개념도 아마 인도나 중국에서 나왔을 것이다. 위의 식을 세로로 곱하는 방법으로 바꾸면 좀 더 쉽게 이해할 수 있다. 간단한 곱하기 4회에 더하기 3회를 해야 한다. 올림이 없는 작은 수를 곱할 때는 각 자릿수를 따로 계산해서 합하기만 하면 된다. 올림이 없는 곱하기 조합은 다음과 같다.
1 x (1~9) = 1~9 → 여기서 19단이 나온 것이다. 앞자리가 항상 1이면 계산이 간단하다.
2 x (1~4) = 2~8
3 x (1~3) = 3~9
2-2. 앞자리만 같은 경우
즉 앞의 특수한 경우로 XY와 XZ의 곱이란 의미다.
X²00 + X(Y+Z)0 + YZ = X0(X0 + Y + Z) + YZ = X0(XY + Z) + YZ = X0(XZ + Y) + YZ
100 + (Y+Z)0 + YZ = 10(10 + Y + Z) + YZ
간단한 곱하기 2회에 더하기 2회로 줄어든다. 19단 계산법은 여기서 나온 것이다. 여기서 앞자리가 1이면 19단인 것이다. 그런데 앞자리가 크면 계산이 힘들어지고 일반적 방법으로 풀어야 한다. 상당히 잡스러운 방법이지? 이걸 뭐 하러 암기하냐?
2-3. 제곱
두 자리 제곱수를 구한다고 하자. 즉 앞의 특수한 경우로 XY와 XY의 곱이란 의미다.
XY² = (X0 + Y)² = X²00 + 2(X*Y)0 + Y² = X0(X0 + 2Y) + Y² = X0(XY + Y) + Y²
56이라면 X=5, Y=6이니 대입해서 계산하면
5²00 + (2*5*6)0 + 6*6 = 2500 + 600 + 36 = 3136
50(56+6) + 36 = 50*62 + 36 = 3100 + 36 = 3136
어느 것이 더 쉬워 보이나? 일반적 방법이 더 쉽다.
2-4. 모든 숫자가 같은 수의 제곱
즉 앞의 특수한 경우로 XX의 형태를 말하는 것이다.
X²00 + 2X²0 + X² = X0(X0 + 2X) + X² =X0(XX+X) + X² = 121X²
99*99 = 9801 = 8100 + 2*810 + 81 = 90(99+9) + 81 = 121*81
그러니까 특수한 상황에 적용하는 공식을 몇 개 암기하면 빠르다는 것인데, 위 어느 방법이나 큰 수를 다시 곱해야 하는 문제가 생긴다. 이걸 피하려면 보수를 이용해야 한다.
2-3. 큰 수 곱하기
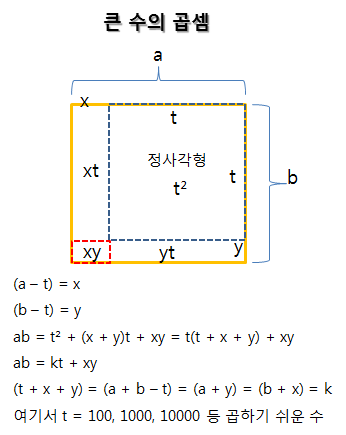
곱하기를 더하기로 바꾸는 방법은 없을까? 보수 이용하기. 앞에서 이미 봤다. 곱하기의 물리적 의미는 면적이다.
a, b = 큰 수, t = 100, 1000, 10000, 50, 500, 5000, 50000 등 a, b에 가까운 수
이건 t의 보수를 이용해서 큰 수를 작은 수로 바꾼 후에 쉬운 곱하기 1회 하고 나머진 덧셈으로 바꾸는 방법이다. 인도 대수학이란다.
a = 84, b = 92, t = 100 이라면
84 → -100 → -16 → 76
92 → -100 → -08 → 76
그러면 x = -16, y = -08, k = 76
76*100 + 16*8 = 7600 + 128 = 7728
보수 표현을 이용하면
11`6`*10`8` = 100*100 + 100(0`8` + 1`6`) + (16)`*(08)` = 10000 - 2400 + 128 = 7728
앞의 2 자릿수 곱하기 와 비교하면? 제곱수 구하기에 사용해 보면? 훨씬 빠르다.
56 → -50 → 6 → 62
62*50 + 6*6 = 3100 + 36 = 3136
음 참으로 신시하군. 푸하하.
★ 나눗셈엔 답이 없다!
학교 산수나, 인도 산수나, 주산이나 계산 방법에 별 차이 없다. 나눌 수 있는 수를 찾아 곱한 후에 빼는 방식을 반복한다. 컴퓨터의 경우는 단순무식하게 반복해서 빼 주는 방법을 사용한다. 곱하기 경우는 99단 암기력을 이용해서 반복 덧셈을 안 해도 되기 때문에 컴퓨터도 사용할 수 있는 방법인데 나눗셈은 모두에게 답이 없다. 지능이 낮은 컴퓨터 경우는 나눌 수 있는 수를 찾는 것도 힘들어 반복 뺄셈을 한다. 현실 세계에서도 공평하게 나누는 건 정말 어렵다. 방법도 없지만, 방법이 있어도 기득권 세력이란 놈들 때문에 힘들다.
계산 결과를 확인할 때 쓰는 방법이라고 하는데 수학적으로 증명하기 정말 어렵다.
※ Digit Sum : 인도 수학에서 각 자릿수를 합하여 점차 1자리로 축소한 것.
예) 666 → 6+6+6=18 → 1+8=9
예) 999 → 9+9+9=27 → 2+7=9
※ Digit란 0,1,2,3,4,5,6,7,8,9 문자 10개를 말 한다.
눈금이 10 단위가 아닌 9단위 자에서 덧셈/곱셈을 하는 것과 같기 때문에
A+B=C에서 C의 나머지는 A, B 나머지의 합(A%9+B%9)에서 다시 나머지를 구한 것과 같아야 한다. 즉 A, B의 Digit Sum의 합은 C의 Digit Sum과 같아야 한다.
A*B=C에서 C의 나머지는 A, B 나머지의 곱(A%9*B%9)에서 다시 나머지를 구한 것과 같아야 한다. 즉 A, B의 Digit Sum의 곱은 C의 Digit Sum과 같아야 한다.
예) 666+999=1665, 18+27=45 → 4+5=9, 1+6+6+5=18 → 1+8=9 일치
예) 666*999=665334, 18x27=486→ 4+8+6=18 → 9, 6+6+5+3+3+4=27 → 2+7=9 일치
아마 어떤 괴짜(아님 바보)가 심심해서 각 자리의 숫자를 다 더하는 짓을 반복하다가 규칙을 발견한 것 같다. 왜 그런지는 수학적으로 증명하기 어렵다.
★ Digit Sum Check 증명!
계산 결과를 확인할 때 쓰는 방법이라고 하는데 수학적으로 증명하기 정말 어렵다.
※ Digit Sum : 인도 수학에서 각 자릿수를 합하여 점차 1자리로 축소한 것.
예) 666 → 6+6+6=18 → 1+8=9
예) 999 → 9+9+9=27 → 2+7=9
※ Digit란 0,1,2,3,4,5,6,7,8,9 문자 10개를 말 한다.
- 0을 제외한 1부터 시작하는 모든 수는 Digit Sum이 1~9로 반복적이다.
- Digit Sum은 9로 나눈 나머지와 같고 Digit Sum은 9진수처럼 반복한다.
- 나머지 1,2,3,4,5,6,7,8,0을 1,2,3,4,5,6,7,8,9로 표기만 바꾸면 Digit Sum이다.
- 나머지를 구하는 연산자를 %라 하자.
- A+B = (9a + A%9) + (9b + B%9) = 9(a+b) + A%9+B%9
- A*B = (9a+A%9) x (9b+B%9) = 9(9ab + bA%9 + aB%9) + A%9*B%9
눈금이 10 단위가 아닌 9단위 자에서 덧셈/곱셈을 하는 것과 같기 때문에
A+B=C에서 C의 나머지는 A, B 나머지의 합(A%9+B%9)에서 다시 나머지를 구한 것과 같아야 한다. 즉 A, B의 Digit Sum의 합은 C의 Digit Sum과 같아야 한다.
A*B=C에서 C의 나머지는 A, B 나머지의 곱(A%9*B%9)에서 다시 나머지를 구한 것과 같아야 한다. 즉 A, B의 Digit Sum의 곱은 C의 Digit Sum과 같아야 한다.
예) 666+999=1665, 18+27=45 → 4+5=9, 1+6+6+5=18 → 1+8=9 일치
예) 666*999=665334, 18x27=486→ 4+8+6=18 → 9, 6+6+5+3+3+4=27 → 2+7=9 일치
아마 어떤 괴짜(아님 바보)가 심심해서 각 자리의 숫자를 다 더하는 짓을 반복하다가 규칙을 발견한 것 같다. 왜 그런지는 수학적으로 증명하기 어렵다.
3. 제곱수 암기 = 면적 계산 = 제곱근표 암기?
제곱근을 계산할 때 제곱수(제곱수 ↔ 제곱근)를 외우고 있으면 도움이 된다. 예를 들어 14²=196, 15²=225를 암기 하고 있다면 2의 제곱근은 200의 제곱근을 구하여 10으로 나누면 되는 문제가 된다. 200은 196 ~ 225 사이다. 고로 아마도 1.4xxx가 될 것이라고 추정할 수 있다. 이제 14X 형태의 숫자로 더욱 가까운 근사치를 구할 수 있다. 이런 경우에는 10단위까지 제곱수를 암기하는 것이 도움이 되겠다. (음 19단인가?)
| 19단 | 제곱 |
| 11 | 121 |
| 12 | 144 |
| 13 | 169 |
| 14 | 196 |
| 15 | 225 |
| 16 | 256 |
| 17 | 289 |
| 18 | 324 |
| 19 | 361 |
암기 공식은 앞에서 본 바와 같이 1X 형태이니 100 + (2*X)0 + X²이다.
11~99까지 소수(prime number)들의 제곱만 외우는 것도 한 방법이다. 모든 수는 소수로 분해되기 때문이다. 여하튼 제곱근을 빨리 구하려면 제곱수를 빨리 구해야 한다. 옛날엔 컴퓨터가 없던 시절이니 무식하게 수학책의 제곱근표를 암기했겠지? 제곱근도 소수만 암기하는 게 현명하겠지.
| 소수 | 제곱근 |
| 2 | 1.41 |
| 3 | 1.73 |
| 5 | 2.24 |
| 6 | 2.45 |
| 7 | 2.65 |
| 10 | 3.16 |
제곱근을 계산할 때는 그것의 물리적 의미가 면적이기 때문에 정사각형 타일로 상상하여 계산하는 방법도 있다. 예를 들어 2제곱근을 구한다고 할 때 10제곱=100배를 하여 200의 제곱근을 구한다고 상상한다. 그러면 200개의 정사각형을 이용해서 하나의 대형 정사각형을 만든다고 상상한다.
위에서 가로 세로 14개의 정사각형으로 대충 큰 사각형을 만들었고 남은 것이 4개다. 1.4XXX까지 구한 것이다. 이 남은 4개를 다시 가로 세로 10배로 하여 400개의 소형 정사각형을 만들고 양변으로 나누어 붙여 본다. 가로 세로 140개의 정사각형을 빼면 400 - 280 = 120개의 정사각형이 나온다. 고로 1.41XX까지 구한 것이다.
4. 단위 환산
달러 & 콤마
동양은 만 단위, 서양은 천 단위라서 콤마 찍는 위치가 헛갈린다. 이런 경우 숫자 위에 동양 단위 콤마(따옴표)를 넣어 보면 쉽게 읽을 수 있다. 동양에서 사용하는 단위가 더 크고 서양은 큰 수를 표현하는 단어가 부족하다. 영미 간에도 단어 뜻에 차이가 있는 걸로 봐선 큰 수에 대한 표현이 정리 되지 못 했다. 거기에 환율에선 1달러와 1천원으로 0이 3개 차이가 있어 더욱 돈 계산이 어렵다.
1,234,567,890,000 = 1t234b567m890,000 = 1조2345억6789만0000 = 1'2345'6789'0000
※ trillion/트릴리언, billion/빌리언, million/밀리언
- 1,000,000,000,000 = 1트릴리언$ = 1조$ → 1천조원
- 1,000,000,000 = 1빌리언$ = 10억$ → 1조원 = 순양함?
- 1,000,000 = 1밀리언$ = 100만$ → 10억원 = 다가구 주택 한 채?
- 1,000 = 1싸우전$ = 1000$ → 100만원 = 최저 임금?
위와 같이 외운다. 트리-비-미-싸, 일조-십억-백만-천, 달러를 원화로 바꿀 때, 잘 보면 자릿수가 한 칸씩 변한다.
※ 다가구 주택 : 4층 이하, 연면적 200평 이하(가구당 50평), 소유 구분 없음(전월세)
※ 다세대 주택 : 4층 이하, 연면적 200평 이하(가구당 50평), 소유 구분 있음
※ 연립 주택 : 4층 이하, 연면적 200평 초과, 소유 구분 있음
※ 아파트 : 4층 이상(엘리베이터 설치), 연면적 200평 초과, 소유 구분 있음
※ 단독 주택 : 다가구 주택
※ 공동 주택 : 다세대 주택, 연립 주택, 아파트
평수 & 제곱미터
땅 면적 계산할 때는 단위가 2개라서 헛갈린다. 1평은 가로 세로 180cm로 2명이 잠 잘 수 있는 공간으로 암기한다. 나머지 환산은 간단하게 303030이란 숫자만 기억하면 된다.
㎡
|
평
|
변(m)
|
| 1 | 0.30303 | 1 |
| 10 | 3.03030 | 3.16 |
| 100 | 30.3030 | 10 |
| 1000 | 303.030 | 31.6 |
| 10000 | 3030.30 | 100 |
| 3.3 | 1 | 1.82 |
| 33 | 10 | 5.74 |
| 330 | 100 | 18.2 |
| 3300 | 1000 | 57.4 |
| 33000 | 10000 | 182 |
영미 단위 vs 국제 단위
영미 단위는 중국 고대 도량형(동양)과 비슷하게 주먹구구식이다. 학교에서 배우는 근대에 만들어진 유럽 프랑스(국제 표준) 단위와 달라서 헛갈린다. 간단하게 암기하고 환산하는 방법이다.
- 1파운드 = 12온스 or 16온스 = 약 450g = 1/2kg – 10%
- 1근 = 600g or 375g = 한 줌/움큼
파운드는 1/2을 해서 kg으로 바꾼 후에 10%를 빼면 된다. 영미 단위는 12진법, 동양은 10진법을 쓴다. 고로 이보다 작은 온스 단위로 가면 계산이 복잡하다. 허나 이 단위에선 중요한 용도가 없기 때문에 무시한다. 상거래에선 금액 차이도 작고, 과학적으로 쓰기엔 너무 정밀하지 못 하기 때문이다. 보통 이 단위에선 그램(g)을 쓴다.
- 10마일 = 16km = 4km * 4 = 40리 = 도보 4시간 거리 (시속 4km)
- 1야드 = 3피트 = 약 90cm = 1m – 10%
- 1피트 = 12인치 = 약 30cm = 1자(척) = 10치(촌)
미터법과 동양 척도와 딱 맞는 10마일, 1야드, 1피트로 암기한다. 야드는 10%만 빼면 그대로 미터와 같다. 피트보다 작은 인치 단위의 경우는 진법 차이로 계산이 복잡하다. 역시 이 단위는 상거래 상의 금액 차이도 적고, 공학적으로 쓰기엔 너무 정밀하지 못 하니 무시한다. 보통 이 단위에선 cm, mm, um를 쓴다.
- 1에이커 = 약 4000㎡ = 약 1200평 = 변 63m(70야드) = 대각 89m(100야드)
면적은 주로 농지 측정에 사용할 것인데 면적에 대한 감이 오지 않을 때는 정사각형으로 보고 제곱근을 외우고 있거나 대각 길이를 외우고 있으면 된다. 대각으로 100미터 달리기를 할 수 있는 정사각형 초등학교 운동장을 상상하면 비슷하다.
- 1리터 = 1000cc(시시) = 물 1kg
- 1시시 = 3제곱센티미터 = 물 1g
- 1말(두) = 10되(승) = 100홉 = 약 18리터
영미도 부피와 시간 단위는 과거에 잘 사용하지 않아서 현대식 단위를 따른다. 부피 대신 무게로 상거래를 했을 것이고, 시간을 측정하는 방법 같은 것은 없었으니까.
5. 상용로그표 암기?
상용로그표를 암기하면 곱셈, 나눗셈을 덧셈, 뺄셈으로 계산할 수 있다. 그런데 상용로그표를 보면 알겠지만 겨우 3~4자리 숫자의 곱셈, 나눗셈을 하는 것에 불과하기 때문에 그냥 주산 암산으로 해결하는 것이 낫다. 실수는 가수부 + 지수부로 분해한다. 그럼 0.xxx * 10ⁿ 형태가 될 것이다. 0.xxx 곱셈은 100자리 곱셈과 같다. 1 이하의 숫자를 곱하면 결과는 1 이하의 0.xxx 형태로 나온다. 고로 100단위 곱셈을 하고 그 결과를 0.xxxxxx 형태로 나타내면 된다.
이런 실수 계산은 실험을 하는 과학자들에게 많이 필요했다. 옛날엔 컴퓨터가 없던 시절이니 무식하게 수학책의 상용로그표를 암기했겠지?
소수
|
로그값
|
2
|
0.30
|
3
|
0.48
|
5
|
0.70
|
7
|
0.85
|
6. 삼각함수표 암기?
실험을 많이 하는 과학자라면 당연히 삼각함수표도 암기했을 것이다. 삼각함수는 45도까지의 x, y 값의 조합만 알면 나머지 각도는 대칭성이 있어 쉽게 구한다. 옛날에는 컴퓨터가 없던 시절이니 무식하게 수학책의 삼각함수표를 암기했겠지?
각도
|
sin
|
cos
|
tan = sin / cos
|
0
|
0.000
|
1.000
|
0.000
|
15
|
0.259
|
0.966
|
0.268
|
30
|
0.500
|
0.866
|
0.577
|
45
|
0.707
|
0.707
|
1.000
|
임의 각을 2등분하는 것은 가능해도 3등분 하는 것은 불가능하다. 고로 직각에서 시작해서 2등분을 반복해서 각도를 구했을 것인데 360도 체계와는 안 맞고 라디안 체계에 더 잘 맞는다. 이것도 고대엔 계산보다는 거대한 원과 격자를 그리고 측정했을 것이다. 정삼각형 작도가 가능하기 때문에 360도를 6등분 하는 건 가능하다.
| a | b | c |
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 7 | 24 | 25 |
| 8 | 15 | 17 |
| 9 | 40 | 41 |
a² + b² = c²
| a | b | c | d |
| 1 | 2 | 2 | 3 |
| 2 | 3 | 6 | 7 |
| 1 | 4 | 8 | 9 |
| 2 | 6 | 9 | 11 |
a² + b² + c² = d² ☞ 물리적 의미가 없어 쓸 일 없을 거다.
또는 제곱근이 들어가지만 정수, 소수(prime number)로만 되어 있는 경우도 암기하면 편하다.
| a | b | c |
| 1 | √2 | √3 |
| 1 | 1 | √2 |
| 1 | 2 | √5 |
| 1 | √3 | 2 |
| 1 | 3 | 2√5 |
7. 60갑자 = 60진법 = 나이 계산
천간 : 갑을.병정.무기.경신.임계 = 5*2 = 10
지지 : 자축.인묘.진사.오미.신유.술해 = 6*2 = 12
| 00 | 10 | 20 | 30 | 40 | 50 | |
+0
|
갑자 | 갑술 | 갑신 | 갑오 | 갑진 | 갑인 |
+1
|
을축 | 을해 | 을유 | 을미 | 을사 | 을묘 |
+2
|
병인 | 병자 | 병술 | 병신 | 병오 | 병진 |
+3
|
정묘 | 정축 | 정해 | 정유 | 정미 | 정사 |
+4
|
무진 | 무인 | 무자 | 무술 | 무신 | 무오 |
+5
|
기사 | 기묘 | 기축 | 기해 | 기유 | 기미 |
+6
|
경오 | 경진 | 경인 | 경자 | 경술 | 경신 |
+7
|
신미 | 신사 | 신묘 | 신축 | 신해 | 신유 |
+8
|
임신 | 임오 | 임진 | 임인 | 임자 | 임술 |
+9
|
계유 | 계미 | 계사 | 계묘 | 계축 | 계해 |
위는 암기표이다. 10진법과 12진법이 결합된 형태이다. 그래서 사람의 띠만 알면 그 사람 나이를 정확하게 추정할 수 있다. 갑(甲)은 10년마다 돌아오니 6번 갑(甲)으로 시작한다. 육갑한다고 할 때의 그 육갑이다. 년도의 끝이 4로 끝나면 갑(甲)으로 시작하는 해이다. 자(子)는 12년마다 돌아오니 5번 자(子)로 끝난다. 여자 이름 같다. 고로 10으로 나누어 나머지만 보면 천간을 결정할 수 있다. 12로 나누어 나머지만 보면 지지를 결정할 수 있으나 나눗셈하기 번거롭다. 12의 10단위 배수는 60=12*5이고, 12의 100단위 배수는 300=12*5*5이기 때문에 300으로 나누고, 60으로 나누고, 12로 나누어 나머지를 보면 천간과 지지를 쉽게 결정할 수 있다.
- 2014 = 2010 + 4 ☞ 일단 4를 뺀다.
- 2010 = 10*201 ☞ 10의 배수이니 갑
- 2010 = 300*6 + 210 ☞ 300으로 나누고 나머지를 구한다.
- 210 = 60*3 + 30 ☞ 60으로 나누고 나머지를 구한다.
- 30 = 12*2 + 6 ☞ 12로 나누고 나머지를 구한다.
- 0,1,2,3,4,5,6 = 자,축,인,묘,진,사,오 ☞ 0부터 센다. 결론 = 갑오년
띠 동갑인데 나는 20대이고 상대는 40대로 보인다면, 자기 나이에 12*2를 더하면 상대의 나이가 바로 나온다.
8. 시간차 계산 = 60진법
시간 계산은 진법이 변해서 어렵다. 초 → 분 → 시는 60진법이다. 시 → 일은 24진법이다. 6을 기본 단위로 하면 6*10이니 시간을 십진법으로 변환 가능하다. 최대 오차 6분, 6초가 있지만 간단하게 시간차를 구할 수 있다.
- 10시15분 - 05시40분 ≒ 10.2시 - 05.6시 = 04.6시 = 04시36분. (1분 오차)
- 48분18초 - 15분50초 ≒ 48.3분 - 15.8분 = 32.5분 = 32분30초. (2초 오차)
아니면 60진법으로 직접 암산해서 정확한 시간차를 구한다. 앞 자리에서 1을 빌리면 60원이 생긴다.
- 10시15분 - 05시40분 = 09시75분 - 05시40분 = 04시35분
- 48분18초 - 15분50초 = 47분78초 - 15분50초 = 32분28초
9. 날짜 요일 계산
일 → 주는 7진법이다. 52주는 364일로 1일이 모자란다.
일 → 월은 개판이다. 28일, 29일, 30일, 31일 중구난방이다.
월 → 년은 12진법이다. 윤년은 2월에 1일이 추가 되어 1년 366일이 된다.
역법이 참 지저분하다. 1주7일은 2주 삭망, 4주1달이라는 음력에서 나온 것이다. 양력과 음력이 일치하지 않아서 양력의 주는 이제 달과 아무 관계도 없다. 관습에 따라 그냥 지저분한 역법을 쓰고 있는 것이다.
- 4의 배수이면 윤년이다.(2000년, 2004년, 2008년…)
- 100의 배수이면 평년으로 고친다.(2000년, 2100년, 2200년…)
- 400의 배수이면 다시 윤년으로 고친다.(2000년, 2400년, 2800년…)
400년마다 큰 사이클이 반복 된다. 400년 동안 윤년은 97년, 평년은 303년이다. 400년 동안 날짜 수는 평년110595 + 윤년35502 = 146097일이다. 이것은 20871주에 해당 된다. 400년 동안의 20871주의 일요일과 날짜 변환만 터득하면 나머지 년도는 반복이다. 이 짓을 잘 해서 TV에 나오는 사람들도 있다. 가끔 컴퓨터와 계산 대결하는 인간들 보면 생각이 나는데, 자동차와 달리기 시합을 하는 것과 뭐가 다르냐? 아무도 자동차와 달리기 시합 안 하잖아? 멍청한 놈이라 취급 받으니까.
농업도 안 되고, 공업도 안 되는 강원도 같은 곳을 먹고 살 수 있게 하는 방법은?
관광업? 산밖에 없는 곳에 뭘 구경하러 오지? 단순히 스키 타러?
강원도 특별 구역에 장벽으로 둘러 싼 매춘 지역, 도박 지역, 대마초 흡연 지역을 만든다. 모든 창녀, 도박장 사업자, 대마초 판매자는 등록을 하고 이 구역에서만 영업을 하며 강원도에 세금을 낸다. 기타 지역에서 영업하면 사형시킨다. 기후가 맞는 지역에선 대마초를 제배해서 의료용 마취제를 제작 판매할 수 있도록 한다.
매춘부는 정기적으로 성병 검사를 받아 깨끗하게 관리 된다. 도박장은 속임수가 없는 공정한 도박을 제공하고 수수료를 받는다. 대마초는 중독성이 없으나 음주 운전처럼 위험할 수가 있으니 통제된 곳에서만 흡연한다. 병원에선 대마초를 마취제로 사용해서 산간 지역 경제 발전에 도움을 준다. 물론 섬유는 밧줄이나 옷을 만들 수도 있다.
이렇게 하면 범죄 집단도 사라지고 강원도 같은 곳도 먹고 살 수 있을 것이다. 좀 더 노골적으로 말하면 강원도가 조폭들이 하던 사업을 흡수하는 것이다.
예부터 산적들은 산에서 살았다.
국가가 제공하는 섹스 복지란?
남녀가 자유롭게 사랑할 저렴한 공간이 거의 없어 주거지에선 아이들도 벽을 넘어 이상한 소리를 듣는다. 아무리 두껍게 공사를 해도 그 소리를 막을 수 없다.
러브텔(사랑방) : 남녀가 환상적 섹스를 즐길 수 있도록 설계된 방음 거울 방으로 특수하게 설계 되어 자신의 엉덩이나 뒤통수를 볼 수 있다. 중앙에는 원형 물침대, 천정에는 도르래도 달려 있어 뭔가 묶어 매달수도 있다. 샤워도 할 수 있고 관장실로 연결 된다.
관장실(화장실) : 화장실로도 쓸 수 있는 곳으로 관장을 하는 곳이다.
처녀방(유리방) : 처녀가 섹스 없이 자신의 순결을 애인에게 증명할 수 있는 곳으로 유리벽으로 구분된 암실이 2개 있다. 하나는 남자용, 다른 하나는 여자용이다.
셀프 누드 촬영실 : 중앙 무대에 발가벗고 서서 포즈를 취하면 사방에서 자동으로 입체 카메라가 360도 촬영하는 시스템이다. (이런 시스템은 카메라를 엄청 많이 설치해야 한다.)
남녀가 자유롭게 사랑할 저렴한 공간이 거의 없어 주거지에선 아이들도 벽을 넘어 이상한 소리를 듣는다. 아무리 두껍게 공사를 해도 그 소리를 막을 수 없다.
러브텔(사랑방) : 남녀가 환상적 섹스를 즐길 수 있도록 설계된 방음 거울 방으로 특수하게 설계 되어 자신의 엉덩이나 뒤통수를 볼 수 있다. 중앙에는 원형 물침대, 천정에는 도르래도 달려 있어 뭔가 묶어 매달수도 있다. 샤워도 할 수 있고 관장실로 연결 된다.
관장실(화장실) : 화장실로도 쓸 수 있는 곳으로 관장을 하는 곳이다.
처녀방(유리방) : 처녀가 섹스 없이 자신의 순결을 애인에게 증명할 수 있는 곳으로 유리벽으로 구분된 암실이 2개 있다. 하나는 남자용, 다른 하나는 여자용이다.
셀프 누드 촬영실 : 중앙 무대에 발가벗고 서서 포즈를 취하면 사방에서 자동으로 입체 카메라가 360도 촬영하는 시스템이다. (이런 시스템은 카메라를 엄청 많이 설치해야 한다.)
어, 6번은 탄젠트는 아닌거 같은데요...ㅎㅎ
답글삭제계산기로 계산해 보세요. 맞아요.
삭제정리해주신 글 도움이 많이 되었습니다. 혹시 주산 공부를 하고 싶다면 어떤 교재나 인강이 좋을까요? 있더라도 너무 유아, 초등용 교재박에 없더라고요,, ㅎㅎ
답글삭제강의/교재는 주로 주산 원리를 가르치는 것이고 여기 내용과 다를 게 없어요.
삭제나머지는 개인의 연습입니다. 학원을 찾아 가시면 되는데 찾기 힘들 겁니다.